我们目前的计算机都是基于冯偌伊曼结构的,在MIMD作为主要研究对象的系统中,分为两种类型:共享内存系统和分布式内存系统,之前我们介绍的基于MPI方式的并行计算编程是属于分布式内存系统的方式,现在我们研究一种基于OpenMP的共享内存系统的并行编程方法。OpenMP是一个什么东东?首先我们来看看来之百度百科中的定义:OpenMp是由OpenMP Architecture Review Board牵头提出的,并已被广泛接受的,用于共享内存并行系统的多处理器程序设计的一套指导性的编译处理方案(Compiler Directive)。OpenMP支持的编程语言包括C语言、C++和Fortran;而支持OpenMp的编译器包括Visual studio,Sun Compiler,GNU Compiler和Intel Compiler等。OpenMP功能中最强大的一个功能是:在我们之前串行程序的源码基础上,只要进行少量的改动,就可以并行化许多串行的for循环,达到明显提高性能的效果。
1.OpenMP环境配置与例子
废话不多少,首先上一个例子,由于本文以Vs 2015作为IDE,C++作为开发语言,在正式进行OpenMP编码之前,需要对编译器稍微配置一下。启动VS2015新建一个C++的控制台应用程序,如下图所示:
然后在项目解决方案资源管理器上选择项目名称,点击右键,选择“属性”,如下图所示:
然后在属性页上左侧选择“配置属性”——“C/C++”——“语言”,然后在右侧“OpenMP支持”后选择“是(/openmp)”,如下图所示:
这样就能在我们VS2015中进行OpenMP的程序开发了。将如下串行程序运行一下
对上面的串行程序增加一句话:#pragma omp parallel for。变为OpenMP的并行,继续运行。
同两次运行时间的对比图如下,可以看出,只要对程序做很少的改动,程序的运行时间就会减少为之前的1/3,性能提升有3倍左右,效果还是蛮好的。
2.基础理论
通过上面的例子,相信大部分同学已经了解了怎么写一个简单的OpenMP的并行计算程序,已经注意到OpenMP的并行计算程序总是以
#pragma omp作为开始的。
在pragma opm后面是一条parallel指令,用来表明之后是一个结构化代码块,最基本的parallel指令可以用如下的形式表示:
#pragma omp parallel如果使用上面这条简单的指令去运行并行计算的话,程序的线程数将由运行时系统决定(这里使用的算法十分复杂),典型的情况下,系统将在每一个核上运行一个线程。如果需要执行使用多少个线程来执行我们的并行程序,就得为parallel指令增加num_threads子句,这样的话,就允许程序员指定执行后代码块的线程数。
#pragma omp parallel num_threads(thread_count)在程序中,为了能够使用OpenMP函数,还需要在程序包含omp.h头文件。
#include在这里,我们还是用之前介绍过的求积分的函数作为例子,
积分函数
数学函数
OpenMP代码
归约
运行:
后面的2指定使用2个线程运行程序。
通过以上的例子,大概知道OpenMP只要添加一条很简单的parallel for指令,就能够并行化大量的for循环所组成的串行程序。但使用它有几天限制条件:
(1)、OpenMP只能并行化for循环,它不会并行while和do-while循环,而且只能并行循环次数在for循环外面就确定了的for循环。
(2)、循环变量只能是整型和指针类型(不能是浮点型)
(3)、循环语句只能是单入口单出口的。循环内部不能改变index,而且里面不能有goto、break、return。但是可以使用continue,因为它并不会减少循环次数。另外exit语句也是可以用的,因为它的能力太大,他一来,程序就结束了。
3.数据依赖问题
使用OpenMP在明面上有上面的这些限制规则,而需要关注的是一个更隐匿的问题:数据依赖问题。这其中涉及两种依赖情况:数据依赖和循环依赖。为了弄清楚这两种依赖的具体是什么,我们先来看一个例子。
计算前n个斐波那契(fibonacci)数:
然后加上OpenMP并行
通过测试,我们有时会得到:
1 1 2 3 5 8 13 21 34 55(正确)
然后也可能偶尔会得到:
1 1 2 3 5 8 0 0 0 0.(错误)
这究竟是发生了什么?似乎运行时,系统将fibo[2], fibo[3], fibo[4], 和 fibo[5]的计算分配给了一个线程,将fibo[6], fibo[7],fibo[8], 和 fibo[9]分配给了另外一个线程。所以在计算fibo[6]的时候,如果第一个线程在此线程之前已经完成,入口初始化为fibo[5]=8,得到的计算结果就是正确的;而如果在计算fibo[6]的时候,如果第一个线程在此线程之前还没有完成,入口初始化为fibo[5]=0,则得到的计算结果就是错误的。
从这里,我们看到两个要点:
(1)OpenMP编译器不检查被parallel for指令并行化的循环所包含的迭代间的依赖关系,而是由程序员来识别这些依赖关系。
(2)一个或更多个迭代结果依赖于其它迭代的循环,一般不能被OpenMP正确的并行化。
从求斐波那契(fibonacci)数的这个例子中,我们发现fibo[3], fibo[4]计算间的依赖关系称之为数据依赖。而fibo[5]的值在一个迭代中计算,它的结果是在之后的迭代中使用,这样的依赖关系称之为循环依赖。
4.怎么寻找循环依赖及解决办法
当我们试图使用一个parallel for指令时,需要小心循环依赖关系,而不用担心数据依赖。例如,在下列循环中:
int i = 0;for (i = 0; i < n; i++){ x[i] = a + i*h; y[i] = exp(x[i]);} 在这个程序中y[i]数据依赖于x[i]的,这种依赖使用OpenMP并行化的话,是没有关系的。
在看一个例子,如下公式计算π:
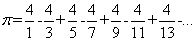
使用能够在串行代码中实现的公式
//第5个案例void blog4::Test5(int argc, char* argv[]){ double factor = 1; double sum = 0.0; int n = 1000; for (int i = 0; i < n; i++) { sum += factor / (2 * i + 1); factor = -factor; } double pi_approx = 4.0*sum; printf("%f", pi_approx);} 得到的结果3.140593,符合预期。我们在上面这个段代码中加上OpenMP的并行化指令
//第5个案例void blog4::Test5(int argc, char* argv[]){ double factor = 1; double sum = 0.0; int n = 1000; int thread_count = strtol(argv[1], NULL, 10);//omp_get_num_threads(); cout << thread_count << endl;#pragma omp parallel for num_threads(thread_count) reduction(+:sum) for (int i = 0; i < n; i++) { sum += factor / (2 * i + 1); factor = -factor; //cout << i << "-" << factor << endl; } double pi_approx = 4.0*sum; printf("%f", pi_approx);} 运行程序
得到结果2.730014,不符合预期。这是存在一个循环依赖,不能保证第k次迭代中对factor的更新对第k+1次迭代有影响,所以导致结果不正确。通过分析,对代码进行相应的改动。
if (i % 2 == 0) factor = 1.0; else factor = -1.0; sum += factor / (2 * i + 1);
运行结果为:2.976587,依旧不正确,为什么呢?
缺省情况下,任何在循环前声明的变量,在线程间都是共享的,。为了消除这种循环依赖关系之外,还需要保证每个线程有它自己的factor副本,OpenMP的语句为我们考虑了,通过添加private子句到parallel指令中来实现这一目标。
//第5个案例void blog4::Test5(int argc, char* argv[]){ double factor = 1; double sum = 0.0; int n = 1000; int thread_count = strtol(argv[1], NULL, 10);//omp_get_num_threads(); cout << thread_count << endl;#pragma omp parallel for num_threads(thread_count) reduction(+:sum) private(factor) for (int i = 0; i < n; i++) { if (i % 2 == 0) factor = 1.0; else factor = -1.0; sum += factor / (2 * i + 1); //factor = -factor; //cout << i << "-" << factor << endl; //SumForNumber(); } double pi_approx = 4.0*sum; printf("%f", pi_approx);} 这下终于正确了。